
快速解 (適用於遞迴函式內呼叫自己 > 1 次)
- 看這個遞迴函式呼叫自己幾次,假設呼叫了
x次 - 看看這個函式的遞迴深度。也就是說這個函式的初始呼叫會需要經過幾次的呼叫自己才會再也沒有任何呼叫,每條路都停止在 base case (終止條件)
- 舉例:可以先看看下面的詳細解,初始呼叫為
u_paths(0, 0),此時u_paths(i + 1, j)需要呼叫m次才會停,u_paths(i, j + 1)需要呼叫n次才會停,所以總共呼叫m + n次才會停,此時遞迴深度h = m + n
- 舉例:可以先看看下面的詳細解,初始呼叫為
- 承上例,此時時間複雜度為
O(x^h)
- 至少目前套用在幾個比較單純的遞迴式都成立,不確定複雜的是不是也成立
- 例子:Validate Binary Search Tree
詳細解 (遞迴樹)
以 Unique Paths 的遞迴解為例:
1 | def uniquePaths(self, m: int, n: int) -> int: |
- 假設
m = 3, n = 2,遞迴樹如下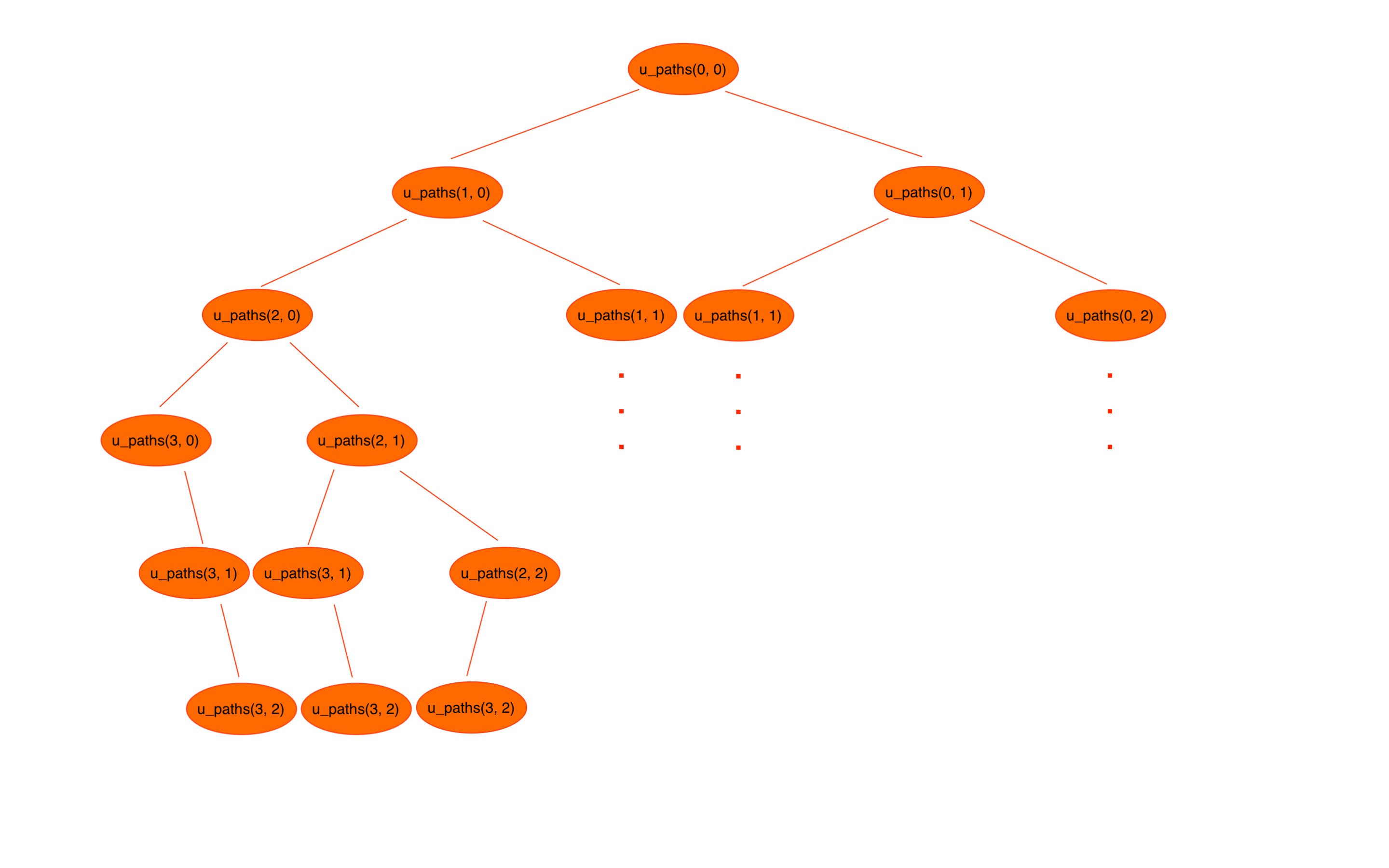
- 由圖可知,遞迴深度為
5 (= m + n)- 要怎麼不用畫圖,用看的就得出深度?
- 深度為根節點走到葉子節點的路徑長,我們可以看從
u_paths(0, 0)開始,要走幾次才會結束:u_paths(i + 1, j)這邊只需要看i,要走i + 1 = 1, 2, ..., m共m次- 走完
m次之後還有u_paths(i, j + 1),要接著再走j + 1 = 1, 2, ..., n共n次 - 所以需要走
m + n次才會結束
- 深度為根節點走到葉子節點的路徑長,我們可以看從
- 要怎麼不用畫圖,用看的就得出深度?
u_paths合併遞迴結果的運算只需要一次加法,可以把時間消耗記做1,也就是每個節點的時間消耗都是1- 所有節點的時間消耗總合就是這個函式的時間複雜度。第一層有
1 (= 2^0)個節點,第二層有2 (= 2^1)個節點,第三層有4 (= 2^2)個節點,以此類推,假設此樹深度為h,所有節點的時間消耗和為2^0 + 2^1 + 2^2 + ... + 2^h,依據等比級數和的公式得出結果為2^(h + 1) - 1- 這邊的算法是假設這是一個滿二元樹來算,但其實這並不是一個滿二元樹 (像第四層就只有
7個節點),所以遞迴樹法並不嚴謹,只是一個估算,真要嚴謹分析的話可以再用 Substitution Method 或 Master Theorem 來驗證 - 由第二點,深度
h = m + n
- 這邊的算法是假設這是一個滿二元樹來算,但其實這並不是一個滿二元樹 (像第四層就只有
- 所以時間複雜度為
O(2^(h + 1)) = O(2 * 2^h) = O(2^h) = O(2^(m + n))